2025-9 理想笔试

要解决这道题，需回忆决策树模型中特征划分与数据纯度提升的衡量指标：

• 选项A（信息增益）：信息增益衡量“特征划分后，数据纯度的提升程度”。它通过“父节点的熵 - 子节点的加权熵”计算，增益越大，说明该特征划分后数据纯度提升越明显，是决策树（如ID3算法）选择特征的核心指标之一。

• 选项B（欧氏距离）：用于衡量样本间的“距离相似性”，常见于聚类、KNN等算法，与决策树的“纯度提升”无关。

• 选项C（余弦相似度）：用于衡量向量间的“方向相似性”，常见于文本相似度等场景，与决策树的纯度提升无关。

• 选项D（均方误差）：是回归问题中衡量预测误差的指标（本题是“是否购买”的分类问题），且与决策树的纯度提升无关。

综上，正确答案为 A。

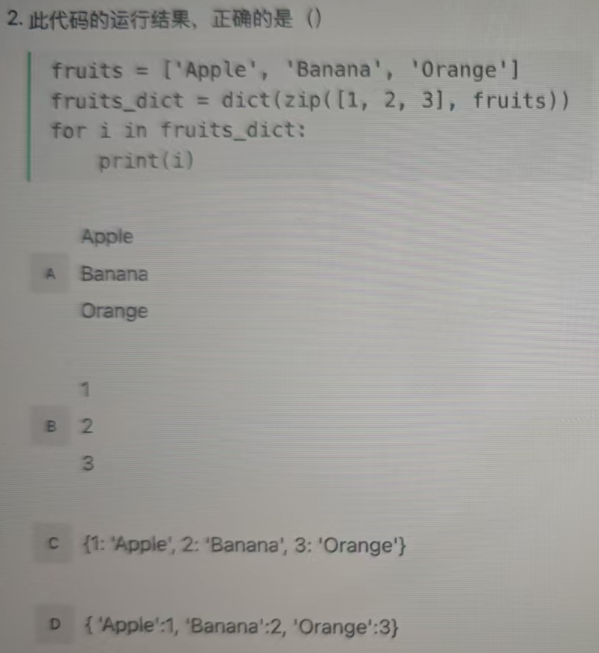
要解决这道题，需逐步分析Python代码的执行逻辑：

代码中：

fruits = ['Apple', 'Banana', 'Orange']
fruits_dict = dict(zip([1, 2, 3], fruits))

• zip([1,2,3], fruits) 会将两个可迭代对象按顺序配对，生成元组 (1, 'Apple'), (2, 'Banana'), (3, 'Orange')。
• dict() 将这些元组转换为字典，因此 fruits_dict 的结果是：{1: 'Apple', 2: 'Banana', 3: 'Orange'}。

代码中：

for i in fruits_dict:
    print(i)

在Python中，遍历字典时，默认遍历的是字典的「键（keys）」。因此，i 会依次取字典的键 1、2、3，print(i) 会依次打印这些键。

最终答案：B

要解决这道题，需明确池化层的核心作用：

池化层（如下采样池化）的主要作用包括：

• 减小图像尺寸，进行数据降维（D选项，通过缩小特征图尺寸，减少后续计算量）；
• 缓解模型过拟合（B选项，减少参数数量，降低模型复杂度）；
• 保持一定的平移不变性（C选项，小范围平移的特征，池化后结果基本一致）。

而上采样是增大图像尺寸的操作（与池化“下采样、缩小尺寸”的逻辑相反），不是池化层的作用。综上，描述“不是池化层作用”的选项是 A。

要计算卷积层输出特征图的大小，需使用二维卷积输出尺寸公式：

对于高度（H）和宽度（W），输出尺寸公式为： $H_{out} = \frac{H_{in} + 2 \times padding_h - kernel_h}{stride_h} + 1$ $W_{out} = \frac{W_{in} + 2 \times padding_w - kernel_w}{stride_w} + 1$

计算高度方向输出 $H_{out}$ 代入公式： $H_{out} = \frac{22 + 2 \times 0 - 22}{1} + 1 = \frac{0}{1} + 1 = 1$

计算宽度方向输出 $W_{out}$ 代入公式： $W_{out} = \frac{750 + 2 \times 63 - 125}{1} + 1$ 先计算分子：$750 + 126 - 125 = 751$ 再计算整体：$\frac{751}{1} + 1 = 752$

因此，卷积层输出的特征图大小为 $(1, 752)$，对应选项 A。

要解决这道题，需明确**多头注意力（MHA）、多查询注意力（MQA）、分组查询注意力（GQA）**的核心区别：

• MHA：每个头都有独立的Query、Key、Value投影，能捕捉细粒度注意力，但计算开销和内存占用高。

• MQA：多个Query头共享一组Key和Value投影，大幅降低计算/内存开销，推理速度快，但可能损失部分表达能力。

• GQA：是MHA与MQA的折中方案——将头分成若干组，每组内的头共享Key和Value投影，在“推理速度、内存使用、表达能力”之间取得平衡。

• 选项A：“GQA通过让一组头共享同一键（Key）和值（Value）投影，在推理速度和内存使用上提供了MHA和MQA之间的一个平衡。” 符合GQA的核心特点（分组共享Key/Value，平衡MHA的“高开销”与MQA的“表达力不足”），正确。

• 选项B：“MQA和GQA都为每个头维护独立的键（Key）和值（Value）投影，但使用不同的合并策略。” 错误。MQA是“多Query头共享Key/Value”，GQA是“分组共享Key/Value”，并非“每个头都独立维护”。

• 选项C：“MQA的计算开销和内存占用高于MHA，但能生成更高质量的输出。” 错误。MQA的设计目的是降低开销（共享Key/Value），因此开销低于MHA；且MHA因“每个头独立投影”，表达力通常更强，输出质量更高。

• 选项D：“GQA的主要目标是大幅提升训练速度，而不是优化推理效率。” 错误。GQA的核心目标是优化推理效率（平衡速度与表达力），而非训练速度。

综上，正确答案为 A。

要解决这个问题，需借助**卡特兰数（Catalan Number）**的概念：

卡特兰数用于计算“n个节点的不同形态二叉树的个数”，其公式为： $C_n = \frac{1}{n+1}\binom{2n}{n}$

其中，卡特兰数的序列为：$C_0=1, C_1=1, C_2=2, C_3=5, C_4=14, \dots$

题目中，先序序列为 a, b, c, d，共4个节点。n个节点的不同二叉树个数对应卡特兰数 $C_{n-1}$（或直接对应n个节点时的卡特兰数 $C_n$，需结合序列长度）。当有4个节点时，对应的卡特兰数为 $C_4 = 14$。

因此，先序序列为 a, b, c, d 的不同二叉树个数是 14，答案为 A。

要解决这个问题，需明确**精确率（Precision）和召回率（Recall）**的计算公式：

• 真正例（TP）：模型预测为“不合格品”，且实际确实是“不合格品”的数量 → 题目中为 $ 8 要解决这个问题，需明确**精确率（Precision）和召回率（Recall）**的计算公式：

1. 定义关键概念

• 真正例（TP）：模型预测为“不合格品”，且实际确实是“不合格品”的数量 → 题目中为 $8$。
• 假正例（FP）：模型错误预测为“不合格品”，但实际是“合格品”的数量 → 题目中为 $2$。
• 假负例（FN）：模型错误预测为“合格品”，但实际是“不合格品”的数量 → 实际不合格品共 $10$ 个，预测对 $8$ 个，故 $FN = 10 - 8 = 2$。

1. 计算精确率（Precision） 精确率描述“模型预测的‘不合格品’中，真正合格的比例”，公式为： $Precision = \frac{TP}{TP + FP}$ 代入数据： $Precision = \frac{8}{8 + 2} = \frac{8}{10} = 80\%$

2. 计算召回率（Recall） 召回率描述“实际的‘不合格品’中，被模型正确预测的比例”，公式为： $Recall = \frac{TP}{TP + FN}$ 代入数据： $Recall = \frac{8}{8 + 2} = \frac{8}{10} = 80\%$

综上，精确率为 $80\%$，召回率为 $80\%$，对应选项 B。。

• 假正例（FP）：模型错误预测为“不合格品”，但实际是“合格品”的数量 → 题目中为 $2$。
• 假负例（FN）：模型错误预测为“合格品”，但实际是“不合格品”的数量 → 实际不合格品共 $10$ 个，预测对 $8$ 个，故 $FN = 10 - 8 = 2$。

精确率描述“模型预测的‘不合格品’中，真正合格的比例”，公式为： $Precision = \frac{TP}{TP + FP}$ 代入数据： $Precision = \frac{8}{8 + 2} = \frac{8}{10} = 80\%$

召回率描述“实际的‘不合格品’中，被模型正确预测的比例”，公式为： $Recall = \frac{TP}{TP + FN}$ 代入数据： $Recall = \frac{8}{8 + 2} = \frac{8}{10} = 80\%$

综上，精确率为 $80\%$，召回率为 $80\%$，对应选项 B。

要解决这个问题，需利用指数分布的极大似然估计方法，步骤如下：

步骤1：回忆指数分布的概率密度 指数分布的概率密度函数为： $f(t;\lambda) = \lambda e^{-\lambda t} \quad (t \geq 0, \lambda > 0)$

步骤2：构造似然函数 已知独立观测值 $t_1=2, t_2=3, t_3=5$，似然函数为各样本密度的乘积： $L(\lambda) = \prod_{i=1}^{3} f(t_i;\lambda) = \lambda e^{-\lambda \cdot 2} \cdot \lambda e^{-\lambda \cdot 3} \cdot \lambda e^{-\lambda \cdot 5}$ 化简得： $L(\lambda) = \lambda^3 e^{-\lambda (2+3+5)} = \lambda^3 e^{-10\lambda}$

步骤3：构造对数似然函数并求导 对似然函数取自然对数（简化求导）： $l(\lambda) = \ln L(\lambda) = 3\ln\lambda - 10\lambda$

对 $\lambda$ 求导，并令导数为0（极大似然估计的核心：导数为0时似然函数最大）： $\frac{dl}{d\lambda} = \frac{3}{\lambda} - 10$

令 $\frac{dl}{d\lambda} = 0$，解得： $\frac{3}{\lambda} - 10 = 0 \implies \lambda = \frac{3}{10} = 0.3$

因此，$\lambda$ 的极大似然估计为 $0.3$，答案为 A。

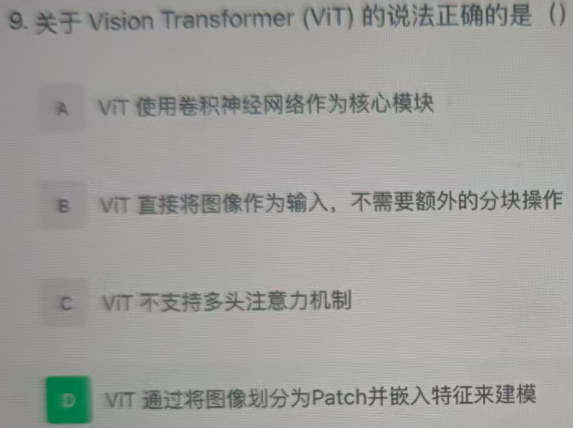
要解决这道题，需明确 Vision Transformer（ViT） 的核心设计原理：

ViT的核心思想是将Transformer架构引入计算机视觉任务，其关键步骤为：

• 先将图像划分为多个小Patch（块）；

• 对每个Patch进行特征嵌入（生成可被Transformer处理的向量序列）；

• 再用Transformer（基于自注意力机制）对这些Patch的特征序列进行建模。

• 选项A：ViT的核心模块是Transformer（自注意力机制），而非卷积神经网络（CNN），因此错误。

• 选项B：ViT必须先将图像分块为Patch，才能转化为Transformer可处理的序列形式，并非“直接输入整图”，因此错误。

• 选项C：ViT内部的Transformer仍然采用多头注意力机制（Multi-Head Attention），这是Transformer的核心机制之一，因此错误。

• 选项D：ViT通过“将图像划分为Patch并嵌入特征”来构建Transformer的输入序列，符合其核心设计，因此正确。

综上，正确答案为 D。

要解决这道题，需明确 直接偏好优化（DPO） 和 近端策略优化（PPO） 在语言模型对齐中的核心区别：

• DPO：直接利用偏好数据（如人类对不同输出的偏好排序）进行概率计算来优化模型，无需训练显式的奖励模型（Reward Model），也避免了强化学习（RL）中复杂的循环过程（如策略梯度更新等）。

• PPO：属于强化学习算法，在语言模型对齐（如RLHF流程）中，依赖独立训练的奖励模型提供奖励信号，进而更新模型策略。

• 选项A：“DPO通过对偏好数据直接进行概率计算来优化策略，避免了训练奖励模型和复杂的强化学习循环；而PPO是强化学习算法，需要依赖奖励模型来更新策略。” 符合两者核心区别：DPO绕开奖励模型与RL循环，PPO依赖奖励模型做RL更新，正确。

• 选项B：“DPO和PPO都严格依赖一个独立训练的奖励模型来提供优化信号。” 错误，DPO不依赖独立的奖励模型。

• 选项C：“PPO的训练稳定性比DPO更高，因为它完全避免了显式的奖励建模过程。” 错误，DPO才是避免显式奖励建模的方法，且DPO训练通常更稳定（减少了RL的不稳定性问题）。

• 选项D：“DPO的主要优势在于其更高的计算效率，但它无法像PPO那样灵活地融入多种人类反馈信号。” 错误，DPO同样能灵活融入人类偏好类反馈信号；且DPO的优势还包括“无需奖励模型、训练更直接”等，并非“无法灵活融入”。

综上，正确答案为 A。

编程1

Tk 有一个长度为n的全负数数组$\{a_1, a_2, ..., a_n\}$。Tk希望你构造一个长度为n的排列$\{b_1, b_2, ..., b_n\}$，使得$a_1 \times b_1 - a_2 \times b_2 - a_3 \times b_3 - \dots - a_n \times b_n$的值尽可能大，并输出该最大值。

输入描述

每个测试文件均包含多组测试数据。 第一行输入一个整数$T(1 \le T \le 10^4)$，表示测试组数。 除此之外，保证单个测试文件的n之和不超过$2 \times 10^5$。 每组测试数据描述如下：

• 第一行输入一个整数$n(1 \le n \le 2 \times 10^5)$，表示数组的长度；
• 第二行输入n个整数$a_1, a_2, ..., a_n (-10^5 \le a_i \le -1)$，表示全负数数组的元素。

输出描述

对于每组测试数据，新起一行。输出一个整数，表示所求的最大值。

示例1

输入

1
3
-5 -3 -1

输出

6

说明

在这个样例中，最佳方案为$b = \{1, 3, 2\}$，此时

• $a_1 \times b_1 = -5 \times 1 = -5$；
• $a_2 \times b_2 = -3 \times 3 = -9$；
• $a_3 \times b_3 = -1 \times 2 = -2$； 将它们代入表达式可得结果为6。

def solve():
    T = int(input())
    results = []
    for _ in range(T):
        n = int(input())
        a = list(map(int, input().split()))
        
        # 第一项固定 a1 * 1
        first = a[0] * 1
        
        # 剩余部分排序
        rest = a[1:]
        rest.sort()  # 绝对值大的负数在前面
        
        # b 的可用值是 [n, n-1, ..., 2]
        b_values = list(range(n, 1, -1))
        
        s = 0
        for ai, bi in zip(rest, b_values):
            s += ai * bi
        
        results.append(str(first - s))
    
    print("\n".join(results))


if __name__ == "__main__":
    solve()

编程2

给定一张包含n个顶点的无根树，顶点编号为1～n。 每个顶点被染成红色或白色，用长度为n的字符串s表示（下标从1开始），其中第i个字符$s_i$为R表示顶点i为红色，为W表示顶点i为白色。

记$f(i)$为顶点i到所有红色顶点的距离之和，即 $f(i) = \sum_{v=1}^{n} [s_v = \text{R}] \times \text{dist}(i, v),$ 其中$\text{dist}(i, v)$表示顶点i与v之间的边的数目，$[s_v = \text{R}]$为指示函数，当$s_v = \text{R}$时值为1，否则为0。

请计算所有顶点$i = 1,2,\dots,n$的$f(i)$。

【名词解释】 无根树：不指定根节点的树，仅关注顶点与边的连通关系。 指示函数：记作$[P]$，当命题$P$成立时值为1，否则为0。

输入描述

第一行输入一个整数$n$（$1 \leq n \leq 2 \times 10^5$），表示树的顶点数量。 第二行输入一个长度为$n$且只由R和W构成的字符串$s$，表示每个顶点的颜色。 接下来$n-1$行，每行输入两个整数$u_i$和$v_i$（$1 \leq u_i, v_i \leq n$；$u_i \neq v_i$），表示一条边连接顶点$u_i$和$v_i$。

输出描述

在一行上输出$n$个整数$f(1), f(2), \dots, f(n)$，以空格分隔。

示例1

输入

5
RWRWR
1 2
2 3
3 4
4 5

输出

6 5 4 5 6

说明

在该样例中，红色顶点集为$\{1,3,5\}$。

• 对于顶点1，$f(1) = 0 + 2 + 4 = 6$；
• 对于顶点2，$f(2) = 1 + 1 + 3 = 5$；
• 对于顶点3，$f(3) = 2 + 0 + 2 = 4$；
• 对于顶点4，$f(4) = 3 + 1 + 1 = 5$；
• 对于顶点5，$f(5) = 4 + 2 + 0 = 6$。

75% 正确率解法

def solve():
    n = int(input())
    s = input().strip()
    g = [[] for _ in range(n+1)]

    for _ in range(n-1):
        u, v = map(int, input().split())
        g[u].append(v)
        g[v].append(u)

    total_red = sum(1 for c in s if c == 'R')
    subcnt = [0] * (n+1)  # 子树红点数
    f = [0] * (n+1)       # f(i)

    # 第一次 DFS，计算子树红点数和 f(1)
    def dfs1(u, p, depth):
        if s[u-1] == 'R':
            subcnt[u] = 1
            f[1] += depth
        for v in g[u]:
            if v == p:
                continue
            dfs1(v, u, depth+1)
            subcnt[u] += subcnt[v]

    dfs1(1, -1, 0)

    # 第二次 DFS，利用换根关系计算 f(i)
    def dfs2(u, p):
        for v in g[u]:
            if v == p:
                continue
            f[v] = f[u] + (total_red - 2*subcnt[v])
            dfs2(v, u)

    dfs2(1, -1)

    print(" ".join(map(str, f[1:])))

if __name__ == "__main__":
    solve()