基于散射信息和元学习的SAR图像飞机目标识别

Scattering Information and Meta-learning Based SAR Images Interpretation for Aircraft Target Recognition

实验选取Harris-Laplace检测器提取散射关键点，使用2×2的卷积框在每点处进行平移，Sobel求导时的窗口大小设为3。最后对这些点进行聚类操作。下图中第1行为原始图像，第2行为对应的角点检测结果，最终对角点检测提取的结果使用K均值算法进行聚类。

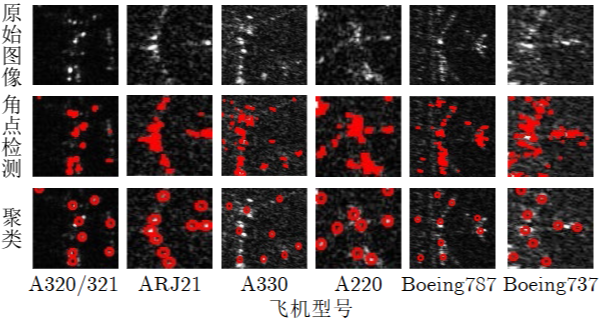
SAR图像易受成像条件的影响，不同朝向的同一型号飞机散射信息可能差异较大，如图4所示。这种差异的存在也有一定意义，由于本文利用的是离散因子差异，当同一型号目标的离散因子差异较大的时候，模型同样会对此类样本对重点关注，因而可以学到类内强泛化性特征表示，这对于提升类内类间的特征表示，增强识别精度也是有意义的。而对于不同型号的目标之间，只要离散因子差异存在，那么相比于基础方法，模型均会增大关注程度，因此对于类间强区分性特征表示和学习并不会产生较大影响。

对提取的角点进行 K-means 聚类，得到 $centers = \{(x_1, y_1), (x_2, y_2), ..., (x_9, y_9)\}$，聚类中心均值定义为$meancenter = (a, b) = (\frac{x_1 + x_2 + ... + x_9}{9} , \frac{y_1 + y_2 + ... + y_9}{9})$

使用平均差来描述离散程度，同时为了将离散度归一化，将聚类点映射到同等大小的图像上，具体过程为$y_2 = \frac{h_2}{h_1} \times y_1, x_2 = \frac{w_2}{w_1} \times x_1$，其中 $(w_1, h_1)$ 和 $(w_2, h_2)$ 分别表示原始图像大小和缩放大小，$(x_1, y_1)$ 和 $(x_2, y_2)$ 分别表示原始坐标和缩放坐标。

最终离散程度$disp$定义为 $disp = \frac{\sqrt{(x_1 - a)^2 + (y_1 - b)^2} + \sqrt{(x_2 - a)^2 + (y_2 - b)^2} + ... + \sqrt{(x_9 - a)^2 + (y_9 - b)^2}}{9}$。

离散因子定义为 $-|disp_q - disp_s|$, $q \in Q, s \in S$，其中 $Q$ 和 $S$ 分别为查询集和支持集。

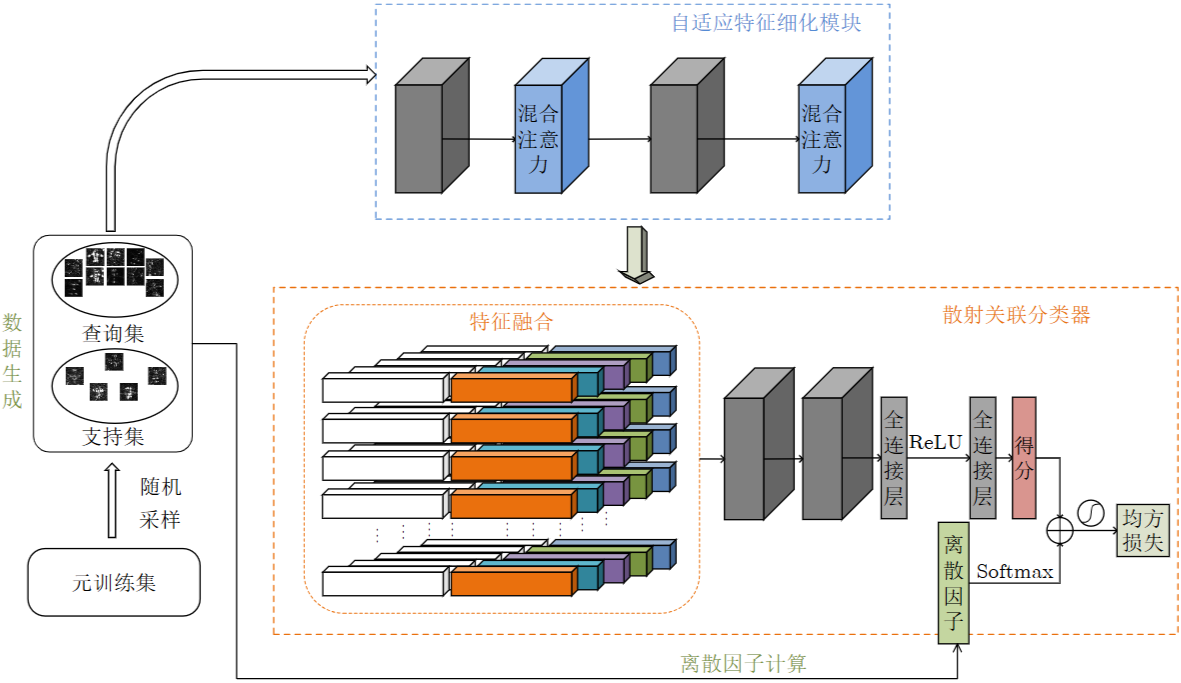
网络最终输出每个查询图片对应于每个类别支持图片的相似度得分。同样，每个查询图片对应于每个类别的支持图片都会计算得到一个离散因子。本文方法将该得分与离散因子相加，并将最终得分输入Sigmoid函数转换为0-1分布

相加的意义是：当属于同一类别的查询图片和支持图片的散射离散程度差异较大的时候，那么可以认为他们属于同一类别的可能性较低，散射关联分类器将其相对得分变小从而使得网络学习更具泛化性的类内特征表示。当属于不同类别的查询图片和支持图片的散射离散程度差异较小的时候，那么可以认为他们属于同一类别的可能性较大，散射关联分类器将其相对得分变大，从而促使网络提取更具有代表性和区分性的类间语义特征。