PROB: Probabilistic Objectness for Open World Object Detection

Zohar, O., Wang, K. C., & Yeung, S. (2023). Prob: Probabilistic objectness for open world object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 11444-11453).

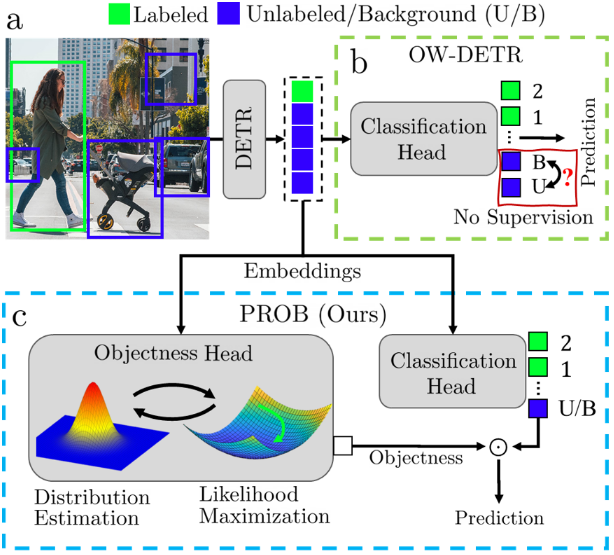
论文的动机：现有的 OWOD 方法的未知对象召回率非常低（∼10%），主要问题是未知物体检测的困难源于缺乏监督，因为与已知物体不同，未知物体没有标记。因此，在训练 OD 模型时，包含未知对象的对象建议将被错误地认为是背景。大多数基于伪标签的 OWOD 方法都试图通过在训练期间使用不同的启发式方法来区分未知对象和背景来克服这一挑战。例如，OW-DETR使用伪标记方案，其中具有高主干特征激活的图像块被确定为未知对象，这些伪标签用于监督 OD 模型。

标准 D-DETR 为每张图像生成一组 N-query 查询嵌入，检测头使用每个嵌入来生成最终预测。将 D-DETR 扩展到开放世界目标需要添加另一个类标签“未知对象”。然而，与其他对象不同的是，未知对象没有标记，因此，在训练时无法区分它们和背景预测。因此，大多数 OWOD 方法都试图识别这些未知对象，并在训练过程中为它们分配伪标签。

相比之下，论文不是分别使用标签和伪标签来推理已知和未知对象，而是采取了更直接的方法，学习一般 “对象性” 的概率模型。

motivation

物体概率建模（Probabilistic Objectness）

传统的做法是直接从背景中识别未知物体，但这样做可能会导致识别错误。为了避免这种情况，论文通过将物体性（是否为物体）和物体类别（分类为已知的某个类别）分开处理。在训练过程中，我们不再需要在训练时识别未知物体。通过分别学习物体性 $p(o|q)$ 和物体类别 $p(l|o, q)$ 。

在推理时：

p(l|q) = \sum_{i=0,1} p(l|o = i, q) \cdot p(o = i|q) = p(l|o = 1, q) \cdot p(o = 1|q)

其中， $p(o=0∣q)=0$ ，即背景的物体性概率为0。这个公式表明分类头 $f_{cls}(q)$ 可以假设已经知道某个查询嵌入是否是物体，而学习如何模仿物体类别的预测。

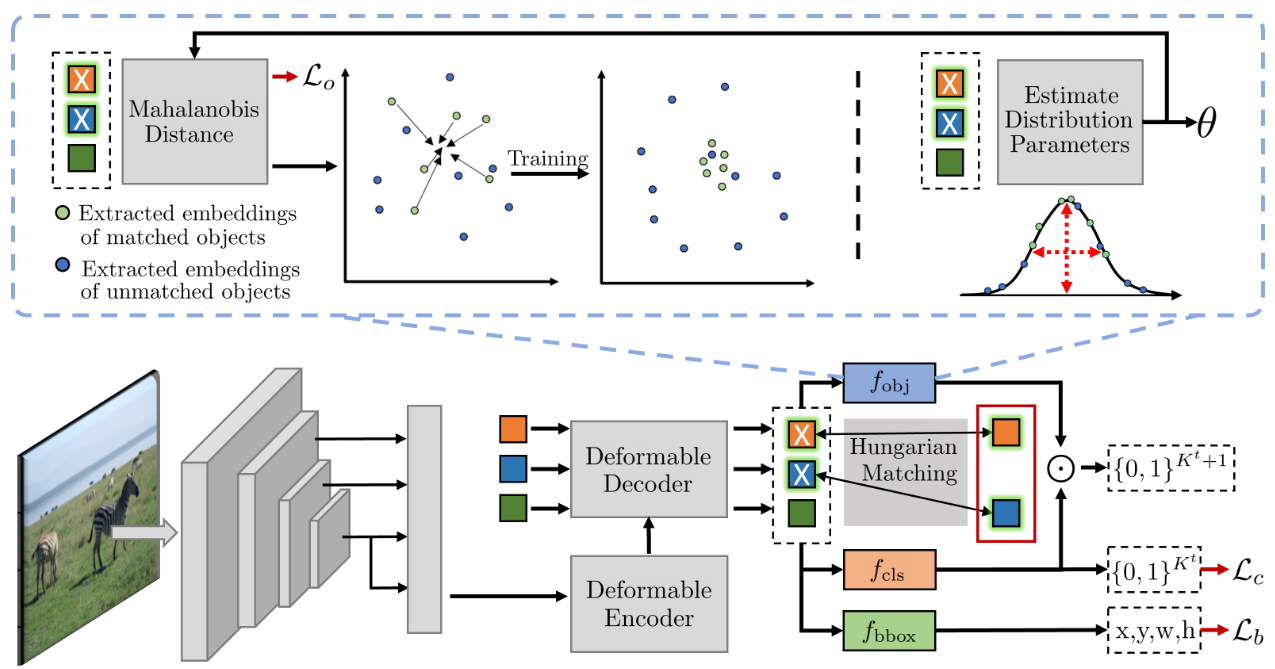
物体性预测模型被设计为一个多元高斯分布 $f_{tobj}(q)$ ，在查询嵌入空间中进行建模，通过计算查询嵌入与该分布的距离来预测物体性。通过马氏距离，模型可以衡量查询嵌入与目标物体特征之间的相似度，进而预测该查询是否是物体。如果query包含物体，那么 $f^t_{obj}(q)$ 应该近似为1

\begin{align} f^t_{obj}(q) = & \exp\left( - (q - \mu)^T \Sigma^{-1} (q - \mu) \right) \\ = & \exp\left( - d_M(q)^2 \right) \end{align}

这里 μ 是查询嵌入的均值，Σ是协方差矩阵， $d_M(q)$ 是查询嵌入的马氏距离，最后预测时分为前向物体背景预测与后向类别预测，将最后一个（第81个）logit训练为未知对象+背景（即，除了已知对象之外的所有内容）logit，然后利用对象性过滤所有背景查询。

p(l|q) = f^t_{cls}(q) \cdot f^t_{obj}(q)

总结一下，

overview

训练过程

训练过程是交替进行的，包括两个步骤：

估计查询嵌入的分布参数（均值和协方差）。
最大化匹配嵌入的似然性，即让物体性预测尽可能准确。

训练的目标是最小化马氏距离：

L_o = \sum_{i \in Z} d_M(q_i)^2

这里的𝑍是与物体匹配的查询嵌入集,训练的目标是使这些距离最小化，从而提高物体性预测的准确性。

note

作者在补充材料中提到，假设通道是 iid 分布式的，在减少训练时间并提高模型稳定性的同时，不会导致性能发生变化。这样在计算马氏距离时计算逆矩阵变得简单，可以化简为计算对角矩阵

\Sigma = I \cdot \sigma

因此最后训练时尽可能让obj分支预测概率为1，即让distance最小化为0：

\begin{align} f^t_{obj}(q) = \exp\left( - d_M(q)^2 \right) \end{align}

obj分支能够输出该query是否是前景还是背景

对象性在增量学习中的作用

在 OWOD 目标中，，OWOD 方法保留了一小部分图像或示例之前的重新训练，以减少灾难性遗忘 [8， 10， 29， 31， 34]。以前的方法随机选择实例与对象，作者认为根据实例的对象性分数主动选择实例有可能进一步提高 OWOD 性能。

在对特定数据集进行训练后，我们计算每个匹配查询embeddings的对象性概率。然后，我们为每个对象类选择前 25 个评分对象。

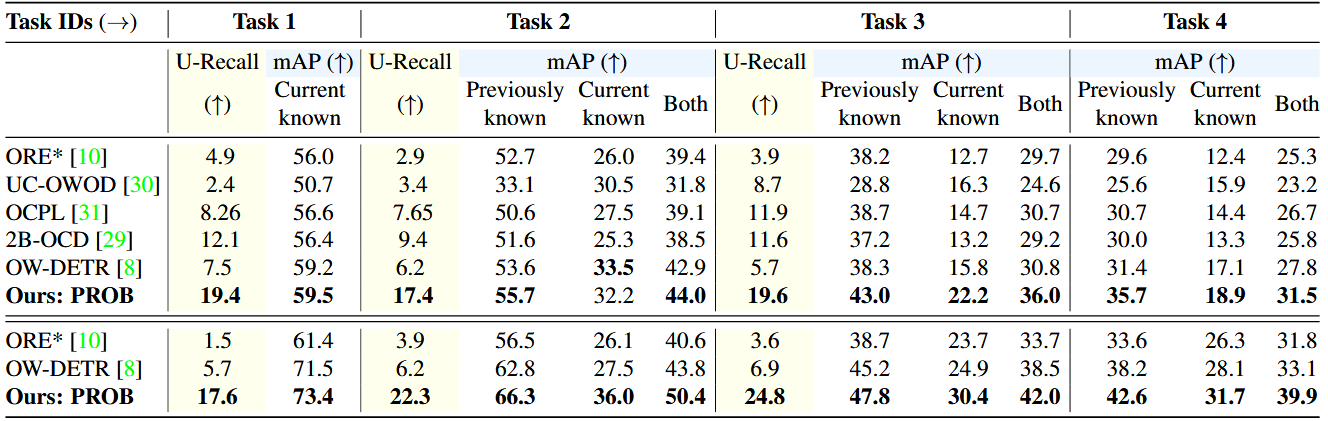
实验结果

experiment

代码分析

关于增量学习的代码

在main_open_world.py中通过exemplar_replay_selection参数控制重放部分是否有效

main_open_world.py
    if args.exemplar_replay_selection:
        image_sorted_scores = get_exemplar_replay(model,exemplar_selection, device, data_loader_train)
        create_ft_dataset(args, image_sorted_scores)

get_exemplar_replay主要实现了通过ExemplarSelection获取对象概率分数

engine.py
@torch.no_grad()
def get_exemplar_replay(model, exemplar_selection, device, data_loader):
    metric_logger = utils.MetricLogger(delimiter="  ")
    header = '[ExempReplay]'
    print_freq = 10
    prefetcher = data_prefetcher(data_loader, device, prefetch=True)
    samples, targets = prefetcher.next()
    image_sorted_scores_reduced={}
    for _ in metric_logger.log_every(range(len(data_loader)), print_freq, header):
        outputs = model(samples)
        image_sorted_scores = exemplar_selection(samples, outputs, targets)
        for i in utils.combine_dict(image_sorted_scores):
            image_sorted_scores_reduced.update(i[0])
            
        metric_logger.update(loss=len(image_sorted_scores_reduced.keys()))
        samples, targets = prefetcher.next()
        
    print(f'found a total of {len(image_sorted_scores_reduced.keys())} images')
    return image_sorted_scores_reduced

未知物体预测头

这里作者在代码中也给出了完整的FullProbObjectnessHead的实现，但是并没有使用，原因是作者在假设特征是 iid 分布的，因此协方差矩阵就简化为公式的形式，这样在减少训练时间并提高模型稳定性的同时，不会导致性能发生变化：

\Sigma = I \cdot \sigma

class ProbObjectnessHead(nn.Module): 
     def __init__(self, hidden_dim): 
         super().__init__() 
         self.flatten = nn.Flatten(0,1) 
         self.objectness_bn = nn.BatchNorm1d(hidden_dim, affine=False) 
  
     def freeze_prob_model(self): 
         self.objectness_bn.eval() 
          
     def forward(self, x): 
         out=self.flatten(x) 
         out=self.objectness_bn(out).unflatten(0, x.shape[:2]) 
         return out.norm(dim=-1)**2 

前向预测

models/prob_deformable_detr.py
outputs_objectnesses = [] 

outputs_objectness = self.prob_obj_head[lvl](hs[lvl]) 

outputs_objectnesses.append(outputs_objectness) 

outputs_objectness = torch.stack(outputs_objectnesses) 

out = {'pred_logits': outputs_class[-1], 'pred_boxes': outputs_coord[-1], 'pred_obj':outputs_objectness[-1]}  

后处理预测

models/prob_deformable_detr.py
obj_prob = torch.exp(-self.temperature*pred_obj).unsqueeze(-1) 
prob = obj_prob*out_logits.sigmoid() 
  
topk_values, topk_indexes = torch.topk(prob.view(out_logits.shape[0], -1), self.pred_per_im, dim=1) 

物体概率建模 （Probabilistic Objectness）​

训练过程​

对象性在增量学习中的作用​

实验结果​

代码分析​

关于增量学习的代码​

未知物体预测头​

前向预测​

后处理预测​