Exploring Orthogonality in Open World Object Detection

Sun, Z., Li, J., & Mu, Y. (2024). Exploring orthogonality in open world object detection. In Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition (pp. 17302-17312).

在常规目标检测框架中，“对象性”判定往往与具体的类别预测紧密绑定。也就是说，模型在判断某个区域是否是“对象”时，通常需要它能被高置信度地归入某个已知类别。这样做的结果是：如果某个对象并不属于训练时已知的类别（即“未知”对象），模型就很可能无法将它判定为“对象”，或者会错误地把它归为某个相似的已知类别。一些对所有对象都普适的通用线索（例如形状、轮廓、结构等）容易被忽略。对那些与已知类别外观差异较大的未知对象，模型更容易漏检或误判。

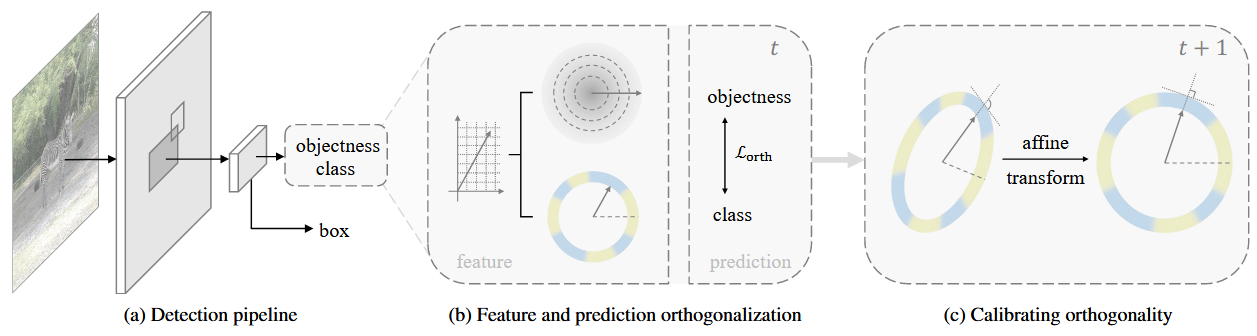
传统方法在特征空间中会将已知对象、未知对象与背景三者的决策边界耦合在一起（如图 1(a) 左侧所示）。这种耦合意味着“是否是对象”与“属于哪个已知类别”被放到了同一条判定线上，当引入新的未知类别时，这条界限很容易受到干扰，导致未知类与已知类的混淆加剧。

因此作者收到下面相关文献的启发，提出需要能够强制在特征空间利用极坐标系将特征进行正交分解成两个部分：大小与方向

Di Chen, Shanshan Zhang, Jian Yang, and Bernt Schiele. Norm-aware embedding for efficient person search. In CVPR, pages 12615–12624, 2020. 2, 3, 4

Weiyang Liu, Zhen Liu, Zhiding Yu, Bo Dai, Rongmei Lin, Yisen Wang, James M Rehg, and Le Song. Decoupled networks. In CVPR, pages 2771–2779, 2018. 2, 3, 4

Yitong Wang, Dihong Gong, Zheng Zhou, Xing Ji, Hao Wang, Zhifeng Li, Wei Liu, and Tong Zhang. Orthogonal deep features decomposition for age-invariant face recognition. In ECCV, pages 738–753, 2018. 2, 3, 4

其中 magnitude 对应于对象性，因为较大的 magnitude 表示更重要的对象，而不同的方向 direction 编码有关已知和未知类的信息。对于那些在direction上无法与已知类别很好对齐、或置信度低的提议（proposal），通过一定的启发式策略（例如设定置信度阈值）将其判定为“未知”。这就为后续的未知类增量学习预留了空间：模型先把它当作“未知对象”保留下来，一旦获得新标签，就能将该方向纳入到已知类别体系中。

为了进一步降低对象性与类别判别的耦合程度，作者还设计了一个“解相关损失”函数，用于惩罚特征中对象性与类别信息的统计相关性。这样，模型在学习时就会倾向于将“是不是对象”与“是什么类别”区分开来，减少对已知类别特征的过度依赖。

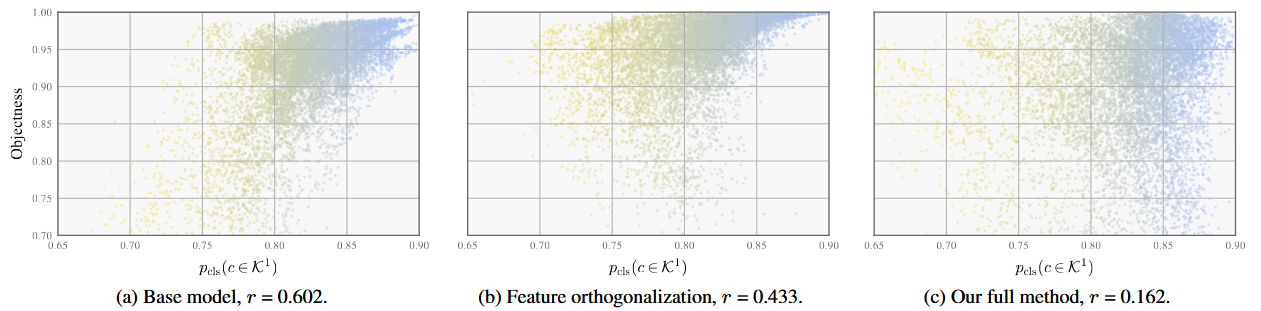
下图是作者的对于物体性与类概率之间的相关性分析。(a)基础模型显示出物体性与已知类概率之间的正相关关系，导致对未知类的召回率较低。(b,c)，结合正交逐步去相关，产生更多的类独立的预测结果

相关性是根据M - OWODB的第一个任务中100张随机图片中每张图片的前100个评分对象提议，用皮尔逊相关系数(记为r)来衡量。

backbone

使用 RandBox（它的特点是移除了区域提案网络，从而产生了类似 Fast R-CNN的架构

具体来说，该模型首先从输入图像中提取特征图，并使用 RoI 池化获得基于随机采样边界框的目标建议特征 f。然后，这些特征被转发到检测头 h 以生成对象性、类别和定位预测。由于我们的工作集中在前两部分（对象性和类别），我们简单地用两个单独的头 $h_obj$ 和 $h_cls$ 来表示检测头 h。对象性和类概率 $p_obj$ 和 $p_cls$ 可以推断为

$$p_{obj} = h_{obj}(f), p_{cls} = h_{cls}(f)$$

$p_cls$被分散到C+1个类中，通过联合概率$p_{joint}=p_{obj} * p_{cls}$判断proposal

特征正交化 Feature orthogonalization

作者从基于极坐标分解的文献中获得灵感，并将物体特征投影为大小和方向两个正交分量。大小单独表示客观性，而方向则用于分类，这样就可以将两个预测过程解耦。

$$p_{\text{obj}} = h_{\text{obj}}(\|\mathbf{f}\|), \quad p_{\text{cls}} = h_{\text{cls}} \left( \frac{\mathbf{f}}{\|\mathbf{f}\|} \right)$$

在作者的代码中：

• obj_feature = cls_feature.norm(...)：提取特征向量的 L2 范数，即幅度，作为“目标性”表征（与论文所述“幅度=目标性”对应）。
• cls_feature = self.norm4(cls_feature)：对特征进行 LayerNorm，去除幅度差异，只保留方向信息，以便分类。

core/head.py

self.norm4 = nn.LayerNorm(d_model)
# ...
obj_feature = cls_feature.norm(dim=-1, keepdim=True)
cls_feature = self.norm4(cls_feature)

为了进一步分离对象性和类预测，从而提高对未知类的性能，作者提出在目标检测器的输出空间中直接执行正交性。通过在损失函数中增加了一个正则项，专门用来“惩罚”二者的线性相关性。

理想状态是“完全独立”（即互信息为 0），但直接最小化互信息在实践中比较困难。因此作者采用了线性相关系数（如相关系数𝜌来衡量二者的相关性，并尝试最小化它。通过对每个类别c与目标性之间的**相关系数（Correlation Coefficient）**做平方求和。若二者无关，该值会接近 0；若二者耦合度高，则该值偏大。

$$L_{\text{orth}} = \sum_c \frac{\text{cov}(p_c, p_{\text{obj}})^2}{\text{var}(p_c) \text{var}(p_{\text{obj}})}$$

相关系数的loss实现如下：

core/loss.py

    def loss_decorr(self, outputs, targets, indices):
        assert self.disentangled != 0
        cls_scores = outputs['pred_logits'].softmax(-1).flatten(0, 1).detach()
        obj_score = outputs['pred_objectness'].reshape(-1)

        cls_mean, obj_mean = cls_scores.mean(dim=0), obj_score.mean()
        cov = ((cls_scores - cls_mean) * (obj_score - obj_mean)[:, np.newaxis]).sum(dim=0)
        var = ((cls_scores - cls_mean) ** 2).sum(dim=0) * ((obj_score - obj_mean) ** 2).sum()
        loss_decorr = (cov ** 2 / var).mean()

        return {'loss_decorr': loss_decorr}

未知类判别

作者采用一种完全基于模型预测的启发式策略来解决这个问题。直觉上，未知对象可以被视为预测置信度较低的异常值，因此可以使用基于置信度的准则进行检测，例如较小的最大softmax概率。这种策略主要通过：先计算模型原始的各类别预测概率，找到最高概率对应的类别，将该类别概率的“补值”分配给“未知类别”，并对剩余概率进行归一化，使所有类别（包含未知类）概率之和为1。

$$p_{\text{cls}} \left( c \in \mathcal{U}^t \right) = p_{\text{cls}}^o \left( c \in \mathcal{K}^t \setminus \{c_{\max}\} \right)$$

core/head.py

class RCNNHead(nn.Module):
    def forward(self, features, bboxes, pro_features, pooler):
        # ...
        # ...


        else:  # feature orthogonality
            # ...

            obj_feature = cls_feature.norm(dim=-1, keepdim=True)
            cls_feature = self.norm4(cls_feature)
            class_logits = self.class_logits(cls_feature)
            class_logit_max = class_logits[:, :-1].max(dim=-1, keepdim=True).values
            class_logits -= class_logit_max
            tmp = class_logits[:, :-1].exp().sum(dim=-1, keepdim=True)
            # assign unknown logit s.t. p(unknown) = p_original(known - max_known)
            unknown_logit = (tmp - 1).log() + tmp.log() - (1 + class_logits[:, -1:].exp()).log()
            class_logits = torch.cat([class_logits[:, :-1], unknown_logit], dim=-1)
            objectness = torch.sigmoid(self.object_logit(obj_feature))

在作者的代码中先取已知类（class_logits[:, :-1]）的最大值 class_logit_max 并将其从所有已知类 logits 中减去，以提高数值稳定性。unknown_logit的计算遵循论文中的推导，并通过对数运算保证稳定性，最终将其拼回到 logits 末尾，得到新的未知类 logit。

core/head.py

class_logits = self.class_logits(cls_feature)
class_logit_max = class_logits[:, :-1].max(dim=-1, keepdim=True).values
class_logits -= class_logit_max
tmp = class_logits[:, :-1].exp().sum(dim=-1, keepdim=True)
# assign unknown logit s.t. p(unknown) = p_original(known - max_known)
unknown_logit = (tmp - 1).log() + tmp.log() - (1 + class_logits[:, -1:].exp()).log()

class_logits = torch.cat([class_logits[:, :-1], unknown_logit], dim=-1)
objectness = torch.sigmoid(self.object_logit(obj_feature))

增量学习

除了在单个阶段中检测开放集对象外，开放世界对象检测还体现了对新对象的增量学习，在增量学习时，如果特征分布因新任务发生大幅变动，也会破坏先前建立的正交化。作者提出的“校准层”（calibration layer）即在此处发挥作用，以维持或恢复正交性。

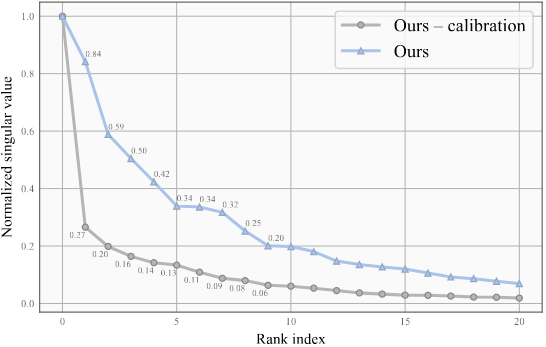
对象性的决策边界可能从超球体转移到超椭球体，并且不再与角度类特征正交。下面的对象特征的奇异值谱展示了这一现象：

• 奇异值更均匀：曲线下降更慢，说明前几阶奇异值与后面奇异值之间的差距没有那么大，特征在各个方向上的方差更加平衡。
• 特征更“球形”或更“各向同性”：在高维空间中，如果特征分布的奇异值更均匀，意味着在各个主成分方向上不会过度集中或过度伸展，可以用更接近球形的决策边界来区分对象。
• 提升未知类别检测：对于开放集检测任务，特征的各向同性有利于在不同方向上识别潜在的未知类；不会因为特征集中在少数方向而在其他方向出现“盲区”。

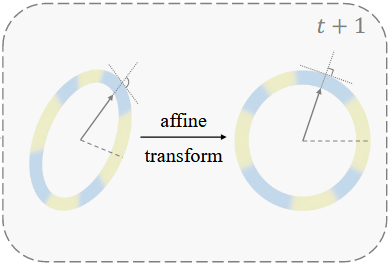
作者提出了一种仿射变换，该变换的核心公式如下，$f_0$表示原始特征（来自主干网络或前一阶段网络的输出）,$M_0$表示第𝑖个任务专属的线性变换（Affine Transformation），也称“校准矩阵”。对于当前新任务𝑡定义$M_t=I$（恒等映射），表示不改变当前任务的特征；而对于过往的任务，可能随着训练进行微调，从而实现对旧特征的重新校准。$w$ 路由向量，用于表示在推理时选用哪个任务的校准映射。通常会是 one-hot 或近似 one-hot 的形式，表示实际只选其中一个分支对应的$M_t$。

$$f = \sum_{i=1}^{t} w_i M_i f^o,$$

为了在推理时选择最合适的校准分支，需要先计算每个分支（对应不同任务）的概率。在文中，作者采用了“最大 softmax probability”的方式来估计任务归属：

$$\pi_i = \frac{\max_{c \in \mathcal{K} \setminus \mathcal{K}^{t-1}} p_c}{Z}, \quad w \sim \text{Cat}(\pi).$$

$\max_{c \in \mathcal{K} \setminus \mathcal{K}^{t-1}} p_c$在任务𝑖所负责的类别范围内，找当前样本的最大预测置信度。如果这个最大置信度比较大，说明该样本更大概率属于任务𝑖。通过一个可微的Gumbel-Max采样过程得到一个one-hot 路由向量 𝑤 只选中一个任务分支）。

然后再利用上面的式子进行特征融合。总结一下：

1. 多分支线性变换的加权和，决定了最终特征来自哪条分支；
2. 根据类别预测来给任务分支打分，形成分支选择的“软概率”；
3. 用 Gumbel-Max 将“软概率”变成“硬选择”（one-hot），并在训练时保留可微性。

core/head.py

# routing within the calibration layer
class_logits = rearrange(class_logits, (b n) c -> b n c', n=len(self.classes))
objectness = rearrange(objectness, '(bn) 1 -> b n 1', n=len(self.classes))
class_logits_splits = torch.spli(class_logits, self.classes, dim=-1)
weight_cat = []
for i in range(len(self.classes)):
    weight_cat.append(class_logits_splits[i][:, i, :].max(dim=-1, keepdim=True)[0])
routing_weights = F.gumbel_softma(torch.cat(weight_cat, dim=-1), dim=-1,hard=True)
routing_weights = routing_weightsunsqueeze(dim=-1)
class_logits = (routing_weights *class_logits).sum(dim=1)
objectness = (routing_weights *objectness).sum(dim=1)

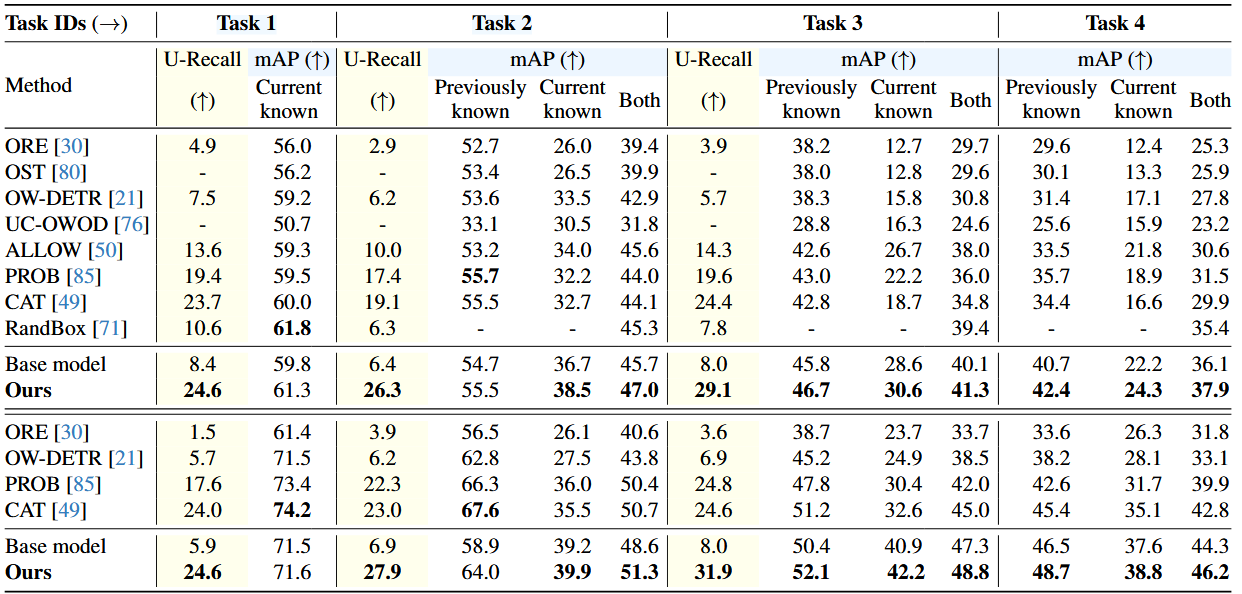
实验结果